ゆとり教育の是非とともに、子供の学力低下問題にからんで、基礎教育がおろそかになっているのではないかという議論がある。 例えば、算数の学習指導要領。 そこできまって槍玉にあがるのが円周率や台形公式である。 円周率を約3で打ち切ってもいいとしているのを基礎教育軽視の象徴だとあげつろう方々が多い。 果たしてそうだろうか。 筆者は3に賛成である。 反対する方々は円周率は3.14でないといけないようだが、これを3.14と決めたのは一体誰であろうか。
いうまでもなく円周率は小数点以下、無限に続く。その数値は10桁程度までならば電卓で「パイ」のキーをたたけば出てくるし、日常生活のうえでも円周率が約3であることを知っていれば支障がないだろう。 たとえば、円筒に紐をまきつける時に、その紐の長さを求めるというような場合である。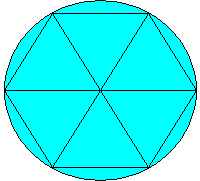
ところで、今年の東大理系の入試問題に円周率が3.05より大きいことを証明せよというのがあったらしい。 円周率は円周の長さと直径の比であるから、その求め方としては、円に内接・外接する正多角形の外周の長さを使う方法が一般的である。 この問題では、円に内接する正八角形や正十二角形を使えばいい。
小学生にも同じ方法で説明するのではなかろうか。 ただし、正八角形や十二角形の外周を小学生が求めるのは無理である。 しかし、正六角形なら簡単だ。 右図のように、正三角形が六つ集まった正六角形の外周は、正三角形の一辺の長さ(円の半径)の6倍、つまり直径の3倍である。 円周の方がこれより少しばかり長いから、円周率が3に極めて近く、それよりちょっと大きいことがすぐわかる。 電卓あり、パソコンありの時代になったのだから、円周率は3.14とバカの一つ覚えする必要は全くないのである。
台形面積の公式もしかり。 三角形の面積の求め方さえ知っていれば充分である。 対角線を引いて台形が二つの三角形の合計であることを見せれば台形の公式なんかへのかっぱである。 それに、日常生活で台形公式を使うようなことに出くわしたことがない。
まあ、義務教育の中に我々の生活に全く不要な公式やらの暗記が多いこと。 算数が嫌いになる子供が多くなるのは無理がない。 自慢ではないがエンジニアである(であった)筆者が、2次方程式の根の公式を使ったことは、何十年という仕事のなかでただの一度もなかった。 こんなことを皆に教えなければならない道理は全くないのである。 それより、生活に必要な算数、例えば、利息とか利回りとかを実感として覚えさせることの方がどれほど大事であることか。 それ以上は専門課程に進んで必要とするもののみに、さらに大事なのは興味をもった子供には、先に先に勉強できるような環境を与えることがいいのである。 (6月4日)